Author: Tianle Yuan

Thermal Dynamics

This section shows the implicit method of thermal transfering with FDE.

Problem background

Think about the 2D case. Considering the continuum of the whole wall material, heat conduction is the major way to transfer heat. We use heat diffusion as our heat conduction method. Assuming that \(X\) is the domain of a 2D plane, \(T\) is the temperature at point \(p\), and \(\alpha\) is the thermal diffusivity, then we have the Equation:

\[ \begin{equation} \frac{\partial T}{\partial t} = \alpha \Delta T(p) = \alpha\left(\frac{\partial^2 T}{\partial x^2}+\frac{\partial^2 T} {\partial y^2}\right),\quad \forall p=(x,y)\in X \label{eq:thermal_diffuse} \end{equation} \]

Take \(f(p)\) as a function relates to point \(p\), which we set is as a constant function. Dirichlet boundary condition is:

\[ \begin{equation} \left\{ \begin{array}{ll} \Delta T(p) =0,\quad\forall p\in X \\ \\ T(p) =f(p),\quad\forall p\in \partial X \end{array} \right. \label{eq:Dirichlet_boundary_condition} \end{equation} \]

Neumann boundary condition is:

\[ \begin{equation} \left\{ \begin{array}{ll} \Delta T(p) =0,\quad\forall p\in X \\ \\ \dfrac{\partial T(p)}{\partial n} =f(p),\quad\forall p\in \partial X \end{array} \right. \label{eq:Neumann_boundary_condition} \end{equation} \]

Five-point stencil discretization

To visualize the phenomenon on a computer, we need to have temperature grids. The grid is used for the discretization of the whole 2D plane. Five-point stencil difference is the method we use to express derivation for the heat partial differential equations. The corresponding temperature grid with a Five-point stencil can be seen in the picture shown below:

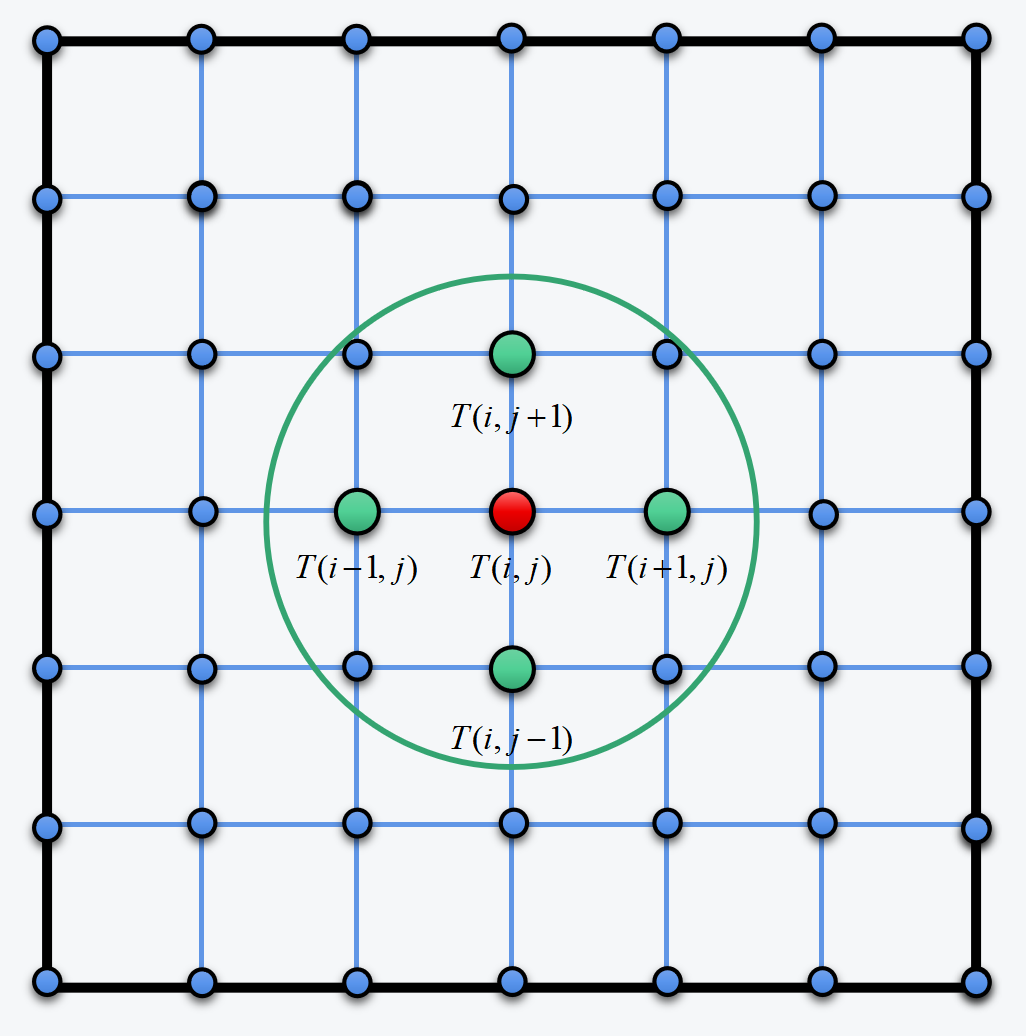
The continuous differential form, shown in the Problem background, is further rewritten into a discrete form by the temperature grid, as shown in the equation below. The sparse matrix system will be solved in an implicit way.

\[ \begin{equation} \begin{aligned} \frac{T^{n+1}_{i,j}-T^{n}_{i,j}}{\Delta t} = & \alpha\left[\frac{T^{n+1}_{i+1,j}-2T^{n+1}_{i,j}+T^{n+1}_{i-1,j}} {\Delta x^2}+\frac{T^{n+1}_{i,j+1}-2T^{n+1}_{i,j}+T^{n+1}_{i,j-1}}{\Delta y^2}\right] \\ &+O(\Delta t,\Delta x^2),\quad \forall (x,y)\in X \label{eq:thermal_diffuse_discrete} \end{aligned} \end{equation} \]

Where \(i\) and \(j\) are the spacial indices on the temperature grid, \(n\) is the temporal index, which monotonically increases over time, and \(o\) is infinitesimal in space and time.

We also do the same discretized processing for the two boundary conditions. We get the expression of Dirichlet B.C. and Neumann B.C. shown in below two equations [Neil 2015].

\[ \begin{equation} T^{n}_{i,j} = C,\quad \forall (x,y)\in \partial X \label{eq:Dirichlet_boundary_condition_discrete} \end{equation} \]

\[ \begin{equation} \left\{ \begin{array}{ll} \frac{T^{n+1}_{i,j}-T^{n}_{i,j}}{\Delta t} = \alpha\left(\frac{2T^{n+1}_{i+1,j}-2T^{n+1}_{i,j}-2\Delta xC} {\Delta x^2}\right),\quad\forall i,\; (i,j)\in \partial X_{left} \\ \\ \frac{T^{n+1}_{i,j}-T^{n}_{i,j}}{\Delta t} = \alpha\left(\frac{2T^{n+1}_{i-1,j}-2T^{n+1}_{i,j}-2\Delta xC} {\Delta x^2}\right),\quad\forall i,\; (i,j)\in \partial X_{right} \\ \\ \frac{T^{n+1}_{i,j}-T^{n}_{i,j}}{\Delta t} = \alpha\left(\frac{2T^{n+1}_{i,j+1}-2T^{n+1}_{i,j}-2\Delta yC} {\Delta y^2}\right),\quad\forall j,\; (i,j)\in \partial X_{top} \\ \\ \frac{T^{n+1}_{i,j}-T^{n}_{i,j}}{\Delta t} = \alpha\left(\frac{2T^{n+1}_{i,j-1}-2T^{n+1}_{i,j}-2\Delta yC} {\Delta y^2}\right),\quad\forall j,\; (i,j)\in \partial X_{bottom} \end{array} \right. \label{eq:Neumann_boundary_condition_discrete} \end{equation} \]

Usually, the Five-point stencil discretization with an explicit method will need to be limited by some step length constraints. However, based on our implementation using the implicit method, our iteration step can be far longer than the explicit method, which means the temperature transferring can be sped up by increasing the length of the iteration step.

Final Results

After setting the initial conditions (I.C.) of temperature and boundary conditions (B.C.), we start iterating the equation system until the solution converges to a stable status. The different iteration processes can be seen below.

Case 1:Dirichlet B.C: top, rightNeumann B.C: bottom, leftHigh temperature I.C: top, rightLow temperature I.C: rest of map

Case 2:Dirichlet B.C: topNeumann B.C: bottom, left, rightHigh temperature I.C: topLow temperature I.C: rest of map

Case 3:Dirichlet B.C: top, rightNeumann B.C: bottom, leftHigh temperature I.C: top, rightLow temperature I.C: rest of map

Case 4:Dirichlet B.C: topNeumann B.C: bottom, left, rightHigh temperature I.C: topLow temperature I.C: rest of map

References

• “Finite difference methods,” Neil Balmforth's webpage. [Online]. Available: https://personal.math.ubc.ca/~njb/fd. [Accessed: 14-Nov-2022].

Comments